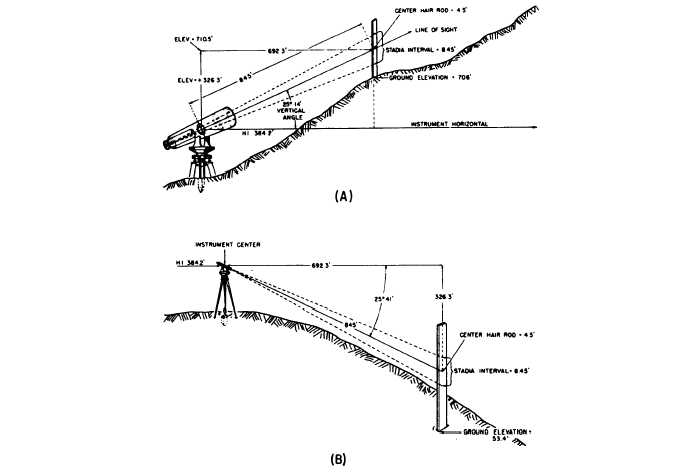
Figure 8-6.—Ground elevations: (A) Telescope raised and (B) telescope depressed.
DISTANCE AND ELEVATION FOR
INCLINED SIGHTS.— The following example will
describe the use of the stadia reduction formulas for
inclined sights. Assume you have a stadia interval of
8.45 and an angle of elevation of 25014’, as shown in
figure 8-6, view A. Let the instrument constant be 1.0.
Substituting the known values in the stadia formula
for the horizontal distance, you have
h=kscos2a +(f+c)cosa
h = 100 (8.45) (0.90458)2 + (1) (0.90458) = 692.34
The horizontal distance is 692 feet.
Substituting the known values in the formula for the
vertical distance, you have
v = 50 (8.45) (0.77125) + (1) (0.42631)
v = 326.28.
The vertical distance to the middle-hair reading on the
rod is 326.28 feet.
To find the elevation of the ground at the base of the
rod, subtract the center-hair rod reading from this
vertical distance and add the height of instrument (HI).
(See fig. 8-6, view A). If the HI is 384.20 feet and the
center-hair rod reading is 4.50 feet, then the ground
elevation is
326.28 - 4.5 + 384.20 = 705.98 feet
If the angle of inclination were depressed, then you
would have to add the center-hair rod reading to the
vertical distance and subtract this sum from the HI. As
you see from figure 8-6, view B, the ground elevation
would be
384.2- (326.28 + 4.5) = 53.42 feet.
STADIA TABLES.— You may save time in finding
the horizontal distance and the vertical distance
(difference in elevation between two points) by using
the stadia reduction tables in appendix II. Here the
8-6