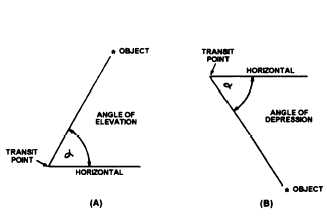
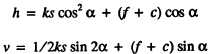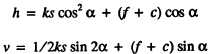Figure 8-4.-(A) Angle of elevation and (B) angle of depression.
The instrument constant is the same for all readings.
Suppose that you are using an externally focusing
instrument with an instrument constant of 1.0. If the
stadia interval is 1 foot, then the horizontal distance is
as follows:
h = (100)(1) + 1 = 101 feet.
If the stadia interval is 2 feet, the horizontal distance is
as follows:
h = (100) (2) + 1 = 201 feet.
Now suppose that you are using an internally
focusing instrument. In this case, the instrument
constant is zero and can be disregarded. This is the
advantage of an internally focusing telescope. So, if the
stadia interval is 1 foot, the horizontal distance is simply
the stadia distance which is 100 feet. For a stadia reading
of 2 feet, the horizontal distance is 200 feet.
Horizontal distance usually is stated to the nearest
foot. Occasionally on short distances (under 300 feet),
it maybe specified that tenths of a foot be used.
Stadia Formulas for Inclined Sights.— -Most often
the sights needed in stadia work are not horizontal. It
may be necessary to incline the telescope upward or
downward at a vertical angle. This vertical angle (a)
may be either an angle of elevation or an angle of
depression, as shown in figure 8-4. If the line of sight is
elevated above the horizontal, you speak of it as an angle
of elevation. If the line of sight is depressed below the
horizontal, the vertical angle is an angle of depression.
In either case, you find the horizontal and vertical
distances by using the following formulas:
These two expressions are called the stadia
formulas for inclined sights in which
h=
v=
h =
a =
f + c =
horizontal distance
vertical distance
stadia distance
vertical angle
instrument constant
Refer to figure 8-5 for clarification of the terms in
the stadia formulas for inclined sights.
Figure 8-5.-Stadia Interval—inclined sight.
8-5