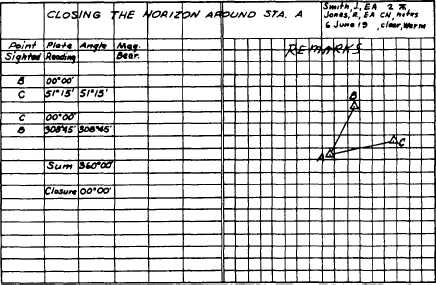
Figure 13-13.-Sample field notes for closing the horizon.
The instrumentman used the same method at
each traverse station, working clockwise around
the traverse to station E. Note that the algebraic
sum of the measured deflection angle (angles to
the right considered as plus, to the left as minus)
is 350°59´. For a closed traverse, the algebraic sum
of the deflection angles from the standpoint of
pure geometry is 360°00´. Therefore, there is an
ANGULAR ERROR OF CLOSURE here of
0°01´. This small error would probably be
considered a normal error. A large variance would
indicate a larger mistake made in the measure-
ments.
In the example just presented, the general
accuracy of all the angular measurements
was checked by comparing the sum of the
deflection angles with the theoretical sum.
The accuracy of single angular measurement
can be checked by the, procedure CLOSING
THE HORIZON. The method is based on
the fact that the theoretical sum of all the
angles around a point is 360°00´.
The field notes in figure 13-13 show the
procedure for closing the horizon. The transit was
set up at station A, and angle BAC was turned,
measuring 51°15´. Then the angle from AC
clockwise around to AB was turned, measuring
308°45´. The sum of the two angles is 360°00´.
The angular error of closure is therefore 0°00´,
meaning that perfect closure is obtained.
Measuring Vertical Angles
The vertical circle and the vertical vernier of
a transit were discussed in chapter 11 of this
training manual. They are used for measuring
vertical angles.
A vertical angle is the angle measured vertically
from a horizontal plane of reference. (See fig.
13-14, view A.) When the telescope is pointed in
the horizontal plane (level), the value of the
vertical angle is zero. When the telescope is
pointed up at a higher feature (elevated), the
vertical angle increases from zero and is a PLUS
VERTICAL ANGLE or ANGLE OF ELEVA-
TION. These values increase from 0° to +90°
when the telescope is pointed straight up.
As the telescope is depressed (pointed down),
the angle also increases in numerical value,
A depressed telescope reading, showing that
it is below the horizontal plane, is a MINUS
VERTICAL ANGLE or ANGLE OF DEPRES-
SION. These numerical values increase from 00
to –90° when the telescope is pointed straight
down.
To measure vertical angles, you must set the
transit upon a definite point and level it. The plate
bubbles must be centered carefully, especially for
transits that have a fixed vertical vernier. The line
of sight is turned approximately at the point; the
horizontal axis is clamped. Then, the horizontal
cross hair is brought exactly to the point by means
of the telescope tangent screw. The angle is read
13-12