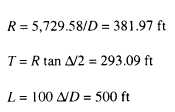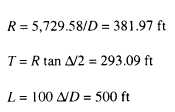length and chord length, or shorter chords are used to
make the error resulting from the difference
negligible. In the latter case, the following chord
lengths are commonly used for the degrees of curve
shown:
100 feet—0 to 3 degrees of curve
50 feet—3 to 8 degrees of curve
25 feet—8 to 16 degrees of curve
10 feet-over 16 degrees of curve
The above chord lengths are the maximum dis-
tances in which the discrepancy between the arc
length and chord length will fall within the allowable
error for taping. The allowable error is 0.02 foot per
100 feet on most construction surveys; however,
based on terrain conditions or other factors, the design
or project engineer may determine that chord lengths
other than those recommended above should be used
for curve stakeout.
The following formulas relate to deflection
angles: (To simplify the formulas and further
discussions of deflection angles, the deflection angle
is designated simply as d rather than d/2.)
Where:
d = Deflection angle (expressed in degrees)
C = Chord length
D = Degree of curve
d = 0.3 CD
Where:
d = Deflection angle (expressed in minutes)
C = Chord length
D = Degree of curve
W h e r e:
d = Deflection angle (expressed in degrees)
C = Chord length
R = Radius.
Figure 11-1O.—Laying out a simple curve.
SOLVING AND LAYING OUT
A SIMPLE CURVE
Now let’s solve and lay out a simple curve using
the arc definition, which is the definition you will
more often use as an EA. In figure 11-10, let’s assume
that the directions of the back and forward tangents
and the location of the PI have previously been
staked, but the tangent distances have not been meas-
ured. Let’s also assume that stations have been set as
far as Station 18 + 00. The specified degree of curve
(D) is 15°, arc definition. Our job is to stake half-sta-
tions on the curve.
Solving a Simple Curve
We will begin by first determining the distance
from Station 18 + 00 to the location of the PI. Since
these points have been staked, we can determine the
distance by field measurement. Let’s assume we have
measured this distance and found it to be 300.89 feet.
Next, we set up a transit at the PI and determine that
deflection angle I is 75°. Since I always equals A, then
A is also 75°, Now we can compute the radius of the
curve, the tangent distance, and the length of curve as
follows:
11-8