radius OIB. From BC, erect a perpendicular
bisector. The point of intersection 02 between
this bisector and the radius OIB is the center
for the arc BC. Draw the radius 02C, and
erect a perpendicular bisector from CD. The
point of intersection 03 of this bisector and
the extension of 02C is the center for the
arc CD.
To continue the curve from D to E, you must
reverse the direction of curvature. Draw the radius
03D, and erect a perpendicular bisector from DE
on the opposite side of the curve from those
previously erected. The point of intersection of
this bisector and the extension of 03D is the center
of the arc DE.
REVERSE, OR OGEE, CURVE
A reverse, or ogee, curve is composed of two
consecutive tangent circular arcs that curve in
opposite directions,
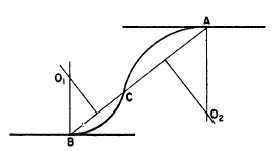
Figure 4-41 shows a method of connecting two
parallel lines by a reverse curve tangent to the
lines. The problem is to construct a reverse curve
tangent to the upper line at A and to the lower
line at B.
Connect A and B by a straight line AB. Select
on AB point C where you want to have the reverse
curve change direction. Erect perpendicular
bisectors from BC and CA, and erect perpen-
diculars from B and A. The points of inter-
section between the perpendiculars (01 and 02)
are the centers for the arcs BC and CA.
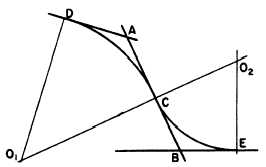
Figure 4-42 shows a method of constructing
a reverse curve tangent to three intersecting
straight lines. The problem is to draw a reverse
Figure 4-41.—Reverse curve connecting and tangent to two
parallel lines.
Figure 4-42.—Reverse curve tangent to three intersecting
straight lines.
curve tangent to the three lines that intersect at
points A and B. Select on AB point C where you
want the reverse curve to change direction. Lay
off from A a distance equal to AC to establish
point D. Erect a perpendicular from D and
another from C. The point of intersection of these
perpendiculars (01) is the center of the arc
DC.
Lay off from B a distance equal to CB
to establish point E. Erect a perpendicular from
E, and extend OIC to intersect it. The point
of intersection (02) is the center of the
arc CE.
NONCIRCULAR CURVES
The basic uniform noncircular curves are the
ellipse, the parabola, and the hyperbola. These
curves are derived from conic sections as shown
in figure 4-43. The circle itself (not shown, but
a curve formed by a plane passed through a cone
perpendicular to the vertical axis) is also derived
from a conic section.
This section describes methods of constructing
the ellipse only. Methods of constructing the
hyperbola are given in Engineering Drawing by
French and Vierck and in Architectural Graphic
Standards.
Of the many different ways to construct
an ellispe, the three most common are as
follows: the pin-and-string method, the four-
center method, and the concentric-circle method.
The method you should use will depend
on the size of the ellipse and where it is to
be used.
4-14