point. It follows that one method of drawing a
line tangent to a circle at a given point is to draw
the radius that intersects the point, and then draw
the line tangent at the point of intersection and
perpendicular to the radius.
Another method is shown in figure 4-32. To
draw a line tangent to the circle at P, set a
compass to the radius of the circle, and, with P
as a center, strike an arc that intersects the circle
at A. With the compass still set to the radius of
the circle, use A as a center and strike an arc that
intersects the first arc at B. With B as a center
and the compass still set to the radius of the
circle, strike another arc. A line through the point
of intersection (0) of the last drawn arc and
through P is tangent to the circle at P.
CIRCULAR ARC OF A
GIVEN RADIUS TANGENT
TO TWO STRAIGHT LINES
Drawing a fillet or round comprises the
problem of drawing a circular arc of a given radius
tangent to two nonparallel lines.
Figure 4-33 shows a method that can be used
when the two nonparallel lines form a right angle.
AB is the given radius of the arc. Set a compass
to this radius, and, with the point of intersection
of the lines as a center, strike an arc intersecting
the lines at C and D. With C and D as centers
and the same radius, strike intersecting arcs as
Figure 4-32.-Line tangent to a given point on a circle.
Figure 4-33.-Circular arc tangent to two lines that form
a right angle.
shown. The point of intersection of these arcs (0)
is the center of the circle of which an arc of the
given radius is tangent to the lines.
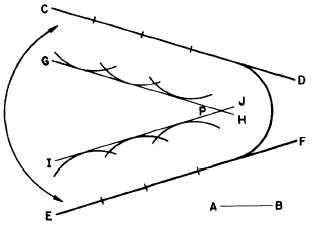
Figure 4-34 shows a method that can be used
regardless of the size of the angle formed by the
lines. Again AB equals the given radius of the arc,
and the problem is to draw an arc with radius
equal to AB, tangent to CD and EF. Draw GH
parallel to CD and at a distance from CD equal
to the given radius of the arc. Draw IJ parallel
to EF and also at a distance equal to the given
radius of the arc. The point of intersection
between GH and IJ (P) is the center of the circle
of which an arc of the given radius is tangent to
CD and EF.
Figure 4-34.-Circular arc tangent to two lines that form
any angle.
4-11