Figure 4-29.-Regular octagon in a given circumscribed
circle.
REGULAR OCTAGON IN A
CIRCUMSCRIBED CIRCLE
GIVEN
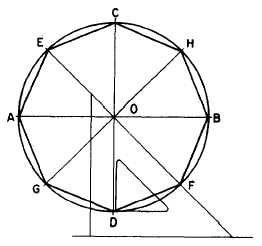
Figure 4-29 shows a method of constructing
a regular octagon in a given circumscribed circle.
Draw horizontal diameter AB and vertical
diameter CD. Use a T square and a 45° triangle
to draw additional diameters EF and GH at 45°
to the horizontal. Connect the points where the
diameters intersect the circle.
REGULAR OCTAGON AROUND
A GIVEN INSCRIBED CIRCLE
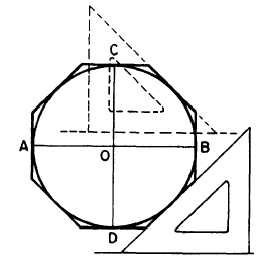
Figure 4-30 shows a method of constructing
a regular octagon around a given inscribed
circle. Draw horizontal diameter AB and vertical
diameter CD. Draw tangents at A, B, C, and D
perpendicular to the diameters. Draw the
remaining sides of the figure tangent to the circle
at 45° to the horizontal.
CIRCULAR CURVES
Many of the common geometrical con-
structions occurring in the drafting room are those
involving circular curves. This section explains
how to construct circular curves that may be
required to satisfy varying conditions.
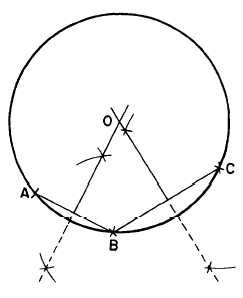
CIRCLE THROUGH THREE POINTS
In figure 4-31 the problem is to draw a circle
(or a circular arc) that passes through points A,
Figure 4-30.-Regular octagon around a
circle.
given inscribed
Figure 4-31.-Circle or arc through three points.
B, and C. Connect the points by lines and erect
perpendicular bisectors as shown. The point of
intersection of the perpendicular bisectors (O) is
the center of the circle or arc passing through all
three points.
LINE TANGENT TO A CIRCLE
AT A GIVEN POINT
A line that is tangent to a circle at a given point
is perpendicular to the radius that intersects the
4-10