REGULAR PENTAGON ON A
GIVEN INSCRIBED CIRCLE
To construct a regular pentagon on a given
inscribed circle, determine the five equal intervals
on the circle in the same manner. However,
instead of connecting these points, draw each side
of the figure tangent to the circle at a point of
intersection.
REGULAR HEXAGON IN A
GIVEN CIRCUMSCRIBED CIRCLE
Many bolt heads and nuts are hexagonal
(six-sided) in shape. Figure 4-26 shows a method
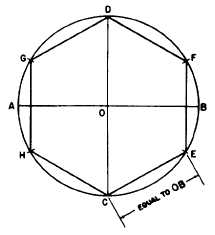
Figure 4-26.-Regular hexagon in a given circumscribed
circle: one method.
Figure 4-27.-Regular hexagon in a given circumscribed
circle: another method.
of constructing a regular hexagon in a given
circumscribed circle. The diameter of the
circumscribed circle has the same length as
the long diameter of the hexagon. The radius
of the circumscribed circle (which equals
one-half the long diameter of the hexagon)
is equal in length to the length of a side.
Lay off the horizontal diameter AB and
vertical diameter CD. OB is the radius of
the circle. From C, draw a line CE equal
to OB; then lay off this interval around
the circle, and connect the points of inter-
section.
Figure 4-27 shows another method of
constructing a regular hexagon in a given
circumscribed circle. Draw vertical diameter AB,
and use a T square and a 30°/60° triangle to draw
BC from B at 30° to the horizontal. Set a
compass to BC, lay off this interval around the
circumference, and connect the points of inter-
section.
REGULAR HEXAGON ON A GIVEN
INSCRIBED CIRCLE
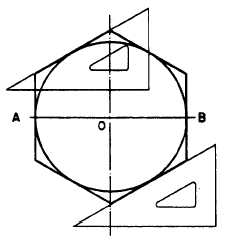
Figure 4-28 shows a method of constructing
a regular hexagon on a given inscribed circle.
Draw horizontal diameter AB and vertical
center line. Draw lines tangent to the circle and
perpendicular to AB at A and B. Use a T square
and a 30°/60° triangle to draw the remaining sides
of the figure tangent to the circle and at 30° to
the horizontal.
Figure 4-28.-Regular hexagon on a given inscribed circle.
4-9