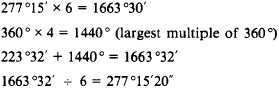then added to the final measurement to obtain the
figure that is to be divided by the total number
of repetitions. In this example,
The mean angle then is
Enter this in the column headed “Mean Angle.”
The following computation shows that you
should use the same method to obtain the mean
closing angle.
In the example shown above, the sum of the
mean angle (82°44´40´´) and the mean closing angle
(277°15´20´´) equals 360°00´00´´. This reflects
perfect closure. In actual practice, perfect angle
closure would be unlikely.
RUNNING A DISTANCE (LINE)
It is often necessary to extend a straight line
marked by two points on the ground. One of the
methods discussed below may be used depending
on whether or not there are obstacles in the line
ahead, and, if so, whether the obstacles are small
or large.
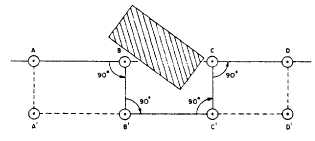
Double Centering or Double Reversing
This method is used to prolong or extend a
line. Suppose you are extending line AB, shown
in figure 13-16. You set up the transit at B,
backsight on A, plunge the telescope to sight
ahead, and set the marker at C´. With the
telescope still inverted, you again sight back on
A; but this time do it by rotating the telescope
through 180°. You then replunge the telescope
and mark the point C´´. Mark the point C halfway
between C´ and C´´. This is the point on the line
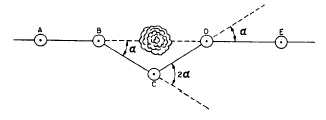
Figure 13-17.-Bypassing a small obstacle by the angle off-
set method.
AB you need to extend. If the instrument is in
perfect adjustment (which seldom happens),
points C´ and C´´ will coincide with point C. For
further extension, the instrument is moved to C
and the procedure repeated to obtain D.
Bypassing an Object by Angle Offset
This method is applied when a tree or other
small obstacle is in the line of sight between two
points. The transit or theodolite is set up at point
B (fig. 13-17) as far from the obstacle as
practical. Point C is set off the line near the
obstacle and where the line BC will clear the
obstacle. At B, measure the deflection angle a.
Move the instrument to C, and lay off the
deflection angle 2a. Measure the distance BC, and
lay off the distance CD equal to BC. Move the
instrument to D, and lay off the deflection
angle a. Mark the point E. Then, line DE is the
prolongation of the line AB.
Bypassing an Object by
Perpendicular Offset
This method is used when a large obstruction,
such as a building, is in the line of sight between
two points. The solution establishes a line parallel
to the original line at a distance clear from the
obstacle, as shown in figure 13-18. The instrument
Figure 13-18.-Bypassing a large obstacle
dicular offset method.
13-15
by the perpen-
Figure 13-16.-Double centering.