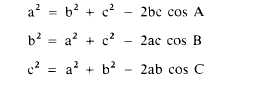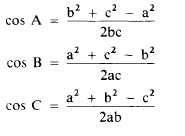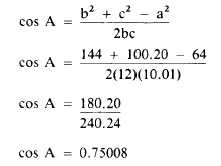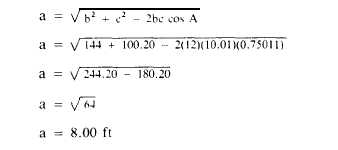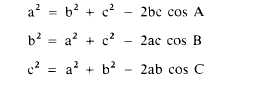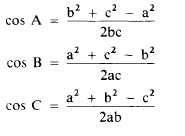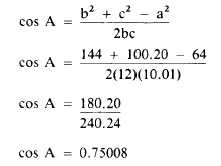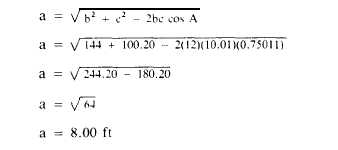Solution by Laws of Cosines
Suppose you know two sides of a triangle and
the angle between the two sides. You cannot solve
this triangle by the law of sines, since you do not
know the length of the side opposite the known
angle or the size of an angle opposite one of the
known sides. In a case of this kind you must begin
by solving for the third side by applying the law
of cosines. The law of cosines is explained and
proved in chapter 5 of NAVPERS 10071-B. If you
are solving for a side on the basis of two known
sides and the known included angle, the law of
cosines states that in any triangle the square of
one side is equal to the sum of the squares of the
other two sides minus twice the product of these
two sides multiplied by the cosine of the angle
between them. This statement may be expressed
in formula form as follows:
For the triangle shown in figure 1-25, you
know that side c measures 10.01 ft; side b,
12.00 ft; and angle A (included between them),
41°24'. The cosine of 41°24' is 0.75011. The
solution for side a is as follows:
Figure 1-25.-Oblique triangle (law of cosines).
Knowing the length of this side, you can now
solve for the remaining values by applying the law
of sines.
If you know all three sides of a triangle, but
none of the angles, you can determine the size of
any angle by the law of cosines, using the follow-
ing formulas:
For the triangle shown in figure 1-26, you
know all three sides but none of the angles. The
solution for angle A is as follows:
The angle with cosine 0.75008 measures (to the
nearest minute) 41°24.
Solution by Law of Tangents
The law of tangents is expressed in words as
follows: In any triangle the difference between two
sides is to their sum as the tangent of half the
difference of the opposite angles is to the tangent
of half their sum.
1-22