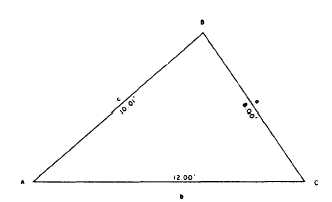
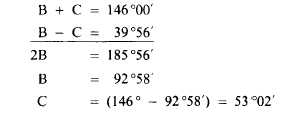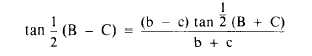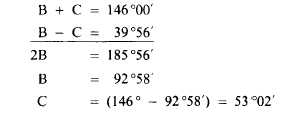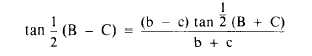Figure 1-26.-Any triangle, three sides given.
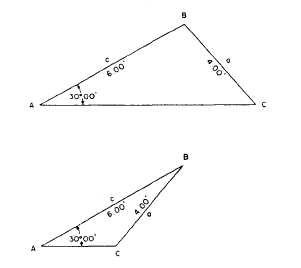
Figure 1-27.-0blique triangle (law of tangents).
For any pair of sides—as side a and side
b—the law may be expressed as follows:
For the triangle shown in figure 1-27, you
know the lengths of two sides and the size of the
angle between them. You can determine the sizes
of the other two angles by applying the law of
tangents as follows.
First note that you can determine the value of
angles (B + C), because (B + C) obviously
equals 180° – A, or 180° – 34°, or 146°. Now,
if you know the sum of two values and the
difference between the same two, you can
determine each of the values as follows:
Now, you know the sum of (B + C).
Therefore, if you could determine the difference,
or (B – C), you could determine the sizes of B
and C You can determine 12(B — C) from the
law of tangents, written as follows:
One-half of (B + C) means one-half of 146°,
or 73°. The tangent of 730 is 3.27085. The
solution for 12(B – C) is therefore as follows:
(from table of natural tangents) 1/2 (B - C)
= 19°58’ (B – C) = 2(19058’) = 39°56’
Knowing both the sum (B + C) and the
difference (B – C), you can now determine the
sizes of B and C as follows:
The Ambiguous Case
When the given data for a triangle consists of
two sides and the angle opposite one of them, it
may be the case that there are two triangles that
conform to the data. A situation in which there
can be two triangles is called the ambiguous case.
Figure 1-28 shows two possible triangles that
Figure 1-28.-Two ambiguous case triangles (solution of one
will satisfy the other).
1-23