As for the transverse Mercator, the conic, and the
gnomonic projections, a glance at the appearance of
meridians and parallels on any one of these indicates
not only that direction is different in different parts of
the map, but that the direction of North (for example)
in one part of the map may be precisely opposite to
that of north in another. Let’s call the two types of
conformality we have mentioned directional con-
formality and distance conformality. Some
authorities hold that directional conformality is all that
is required for a conformal projection. A Mercator
projection has this type of conformality, and this fact
makes that type of projection highly advantageous for
navigational charts. A navigator is primarily
interested in determining geographical location of his
ship; and the principal disadvantage of Mercator
projection—the north-south compared to east-west
distance distortion (which increases with latitude)–is
negligible in navigational practice. This statement
applies only to navigation in customary latitudes,
however, since Mercator projection of the polar
regions (above about 80-degrees latitude) is
impossible.
For surveying and other purposes in which dis-
tance measurements must be consistent in every direc-
tion, Mercator projection presents disadvantages. To
understand these, you have only to reflect on the fact
that no distance scale could be consistently applied to
all parts of a Mercator projection, which means that
no square grid system could be superimposed on a
Mercator projection; however, the transverse
Mercator projection, as it is used in conjunction with
the UTM military grid, provides relatively small-area
maps that are virtually conformal, both direction-wise
and distance-wise.
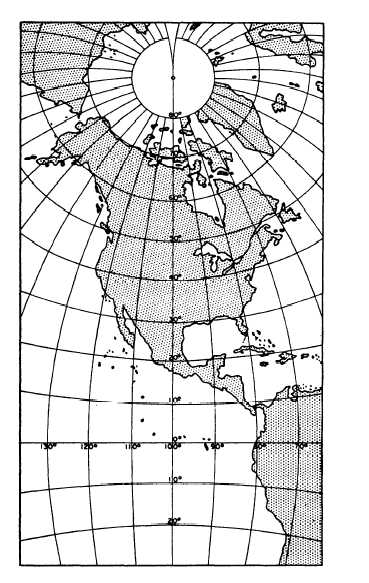
POLYCONIC PROJECTION
In polyconic projection a near approach to
direction conformality is obtained in relatively small-
area maps by projecting the area in question onto more
than one cone. A central meridian on the map is
straight; all the others are slightly curved and not quite
parallel. Similarly, the parallels are slightly curved
and not quite parallel; therefore, they are not precisely
perpendicular to the meridians. An example of a
polyconic map projection is shown in figure 9-24.
Polyconic projection is extensively used for the
quadrangle maps (familiarly called quad sheets) of
areas of the United States published by the Geological
Survey. For most of the built-up areas of the States,
these maps are available on a scale of 1:24,000,
Figure 9-24.—Polyconic projection of North America.
showing areas extending for 7°30’ of latitude and
longitude. An index map is available, which gives
you the quadrangle divisions and the name of the map
that covers a particular area.
That polyconic projection is not conformal
distance-wise is indicated by the fact that one of these
quad sheets, though it shows an area that is square on
the ground, is oblong rather than square. The vertical
or latitudinal length of the map is always greater than
the horizontal or longitudinal length. The reason is
that latitude is measured along a meridian, which is
always a great circle, while longitude is measured
along a parallel; and every parallel other than the
equator is less than a great circle.
An understanding of the concept of the great circle
is essential to a thorough understanding of map and
9-21