triangle CBD, tan B = 1,250/10,000, or 0.125000;
therefore, angle B measures 7°7´30´´. Determining the
distance from the dotted line to the edge of the
approach zone at any station is similarly a simple
right-triangle solution. Suppose that AB is located at
station 0 + 00. Then at station 1 + 00, the distance
from the dotted line to the edge of the approach zone
is 100 tan 7°7´30´´, or 12.5 feet; therefore, the distance
between the center line and the edge of the approach
zone at this station is 750 + 12.5, or 762.5 feet.
To check for obstructions, you must setup a transit
at the narrow end of the approach zone, set the
telescope at a vertical angle equal to the one that the
glide plane makes with the horizontal, and take
observations over the whole approach zone, as
indicated in figure 10-27. Determining the vertical
angle is a simple right-triangle solution. If the glide
angle is 50:1, then the tangent of the vertical angle is
1/50, or 0.020000, and the angle measures 1°8´45´´.
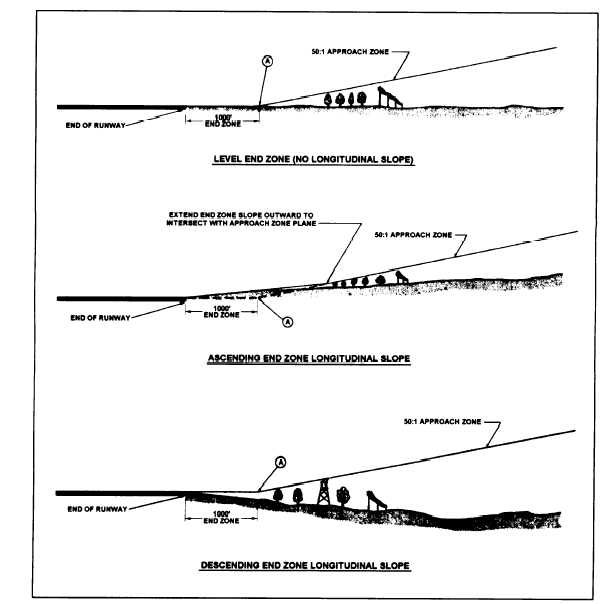
Figure 10-27 shows how the exact vertical
location of the glide plane varies with the character of
the surface of the end zone.
WATERFRONT SURVEYS
Under some circumstances it is possible to chain
distances over the water; however, it is usually more
Figure 10-27.—Approach clearance for different types of end zones.
10-26