Figure 5-30.--Origin of azimuth circle.
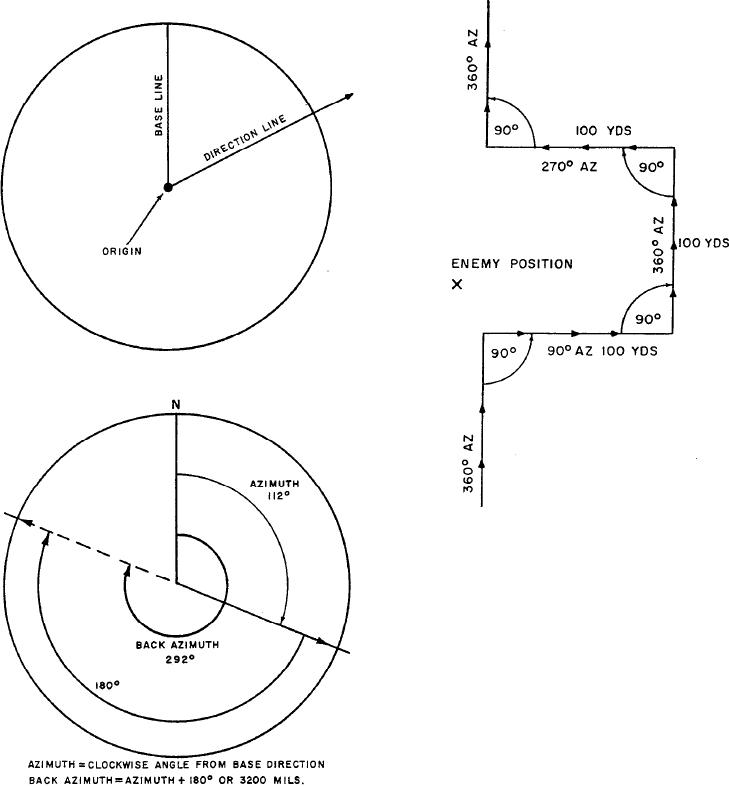
Figure 5-32.--Detour around enemy positions or obstacles.
the back azimuth is the forward azimuth minus 180.
For example, if the forward azimuth of a line is 112
(fig. 5-31), the back azimuth is as follows:
112 + 180 = 292
When the forward azimuth of a line is 310, the back
azimuth is as follows:
310 - 180 = 130
Figure 5-32 shows an example of how to bypass
enemy positions or obstacles by detouring around them.
This allows you to stay oriented by moving at right
Figure 5-31.--Azimuth and back azimuth.
angles for specified distances. For example, if you are
moving on an azimuth of 360 and wish to bypass an
the center of the azimuth circle (fig. 5-30). Azimuths
obstacle or position, you change direction to 90 and
take their name from the base line from which they have
travel for 100 yards; change direction back to 360 and
been measured; true azimuths from true north, magnetic
travel for 100 yards; change direction to 270 and travel
azimuths from magnetic north, and grid azimuths from
for 100 yards; then change direction to 360; and you
grid north (fig. 5-21). Therefore, any one given direction
are back on your original azimuth
can be expressed in three different ways: a grid azimuth,
Bypassing an unexpected obstacle at night is a fairly
when measured on a military map; a magnetic azimuth,
simple matter. To make a 90 turn to the right, hold the
when measured by a compass; or a true azimuth, when
compass as described earlier in the method for night use;
measured from a meridian of longitude.
The BACK AZIMUTH of a line is its forward
turn until the center of the luminous letter E is under the
azimuth plus 180; or if this sum is greater than 360,
luminous line (do NOT change the setting of the
5-22

