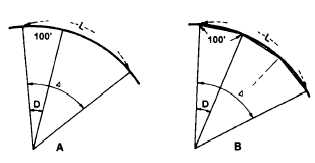
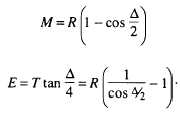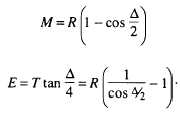Figure 11-8.-Length of curve.
Then, solving for L,
This expression is also applicable to the chord
definition. However, L., in this case, is not the true arc
length, because under the chord definition, the length
of curve is the sum of the chord lengths (each of which
is usually 100 feet or 100 meters), As an example, if,
as shown in view B, figure 11-8, the central angle (A)
is equal to three times the degree of curve (D), then
there are three 100-foot chords; and the length of
“curve” is 300 feet.
Middle Ordinate and
External Distance
Two commonly used formulas for the middle
ordinate (M) and the external distance (E) are as
follows:
DEFLECTION ANGLES
AND CHORDS
From the preceding discussions, one may think
that laying out a curve is simply a matter of locating
the center of a circle, where two known or computed
radii intersect, and then swinging the arc of the
circular curve with a tape. For some applications, that
can be done; for example, when you are laying out the
intersection and curbs of a private road or driveway
with a residential street. In this case, the length of the
radii you are working with is short. However, what if
you are laying out a road with a 1,000- or 12,000- or
even a 40,000-foot radius? Obviously, it would be
impracticable to swing such radii with a tape.
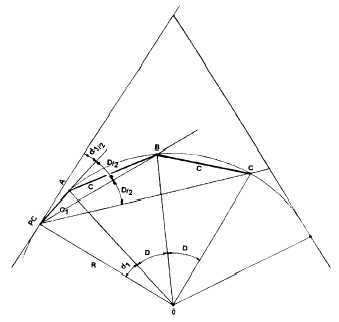
In usual practice, the stakeout of a long-radius
curve involves a combination of turning deflection
angles and measuring the length of chords (C, Cl, or
CZ as appropriate). A transit is set up at the PC, a sight
is taken along the tangent, and each point is located by
turning deflection angles and measuring the chord
distance between stations. This procedure is
illustrated in figure 11-9. In this figure, you see a
portion of a curve that starts at the PC and runs through
points (stations) A, B, and C. To establish the location
of point A on this curve, you should set up your
instrument at the PC, turn the required deflection
angle (all/2), and then measure the required chord
distance from PC to point A. Then, to establish point
B, you turn deflection angle D/2 and measure the
required chord distance from A to B. Point C is located
similarly.
As you are aware, the actual distance along an arc
is greater than the length of a corresponding chord;
therefore, when using the arc definition, either a
correction is applied for the difference between arc
Figure 11-9.-Deflection angles and chords.
11-7