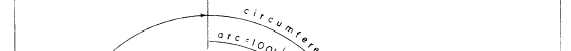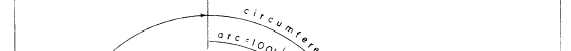E
M
D
c?
The subchord distance between the last
station on the curve and the PT.
EXTERNAL DISTANCE. The external
distance (also called the external secant) is the
distance from the PI to the midpoint of the
curve. The external distance bisects the interior
angle at the PI.
MIDDLE ORDINATE. The middle ordinate is
the distance from the midpoint of the curve to
the midpoint of the long chord. The extension
of the middle ordinate bisects the central angle.
DEGREE OF CURVE. The degree of curve
defines the sharpness or flatness of the curve.
DEGREE OF CURVATURE
The last of the elements listed above (degree of
curve) deserves special attention. Curvature may be
expressed by simply stating the length of the radius of
the curve. That was done earlier in the chapter when
typical radii for various roads were cited. Stating the
radius is a common practice in land surveying and in
the design of urban roads. For highway and railway
work, however, curvature is expressed by the degree
of curve. Two definitions are used for the degree of
curve. These definitions are discussed in the following
sections.
Degree of Curve (Arc Definition)
The arc definition is most frequently used in high-
way design. This definition, illustrated in figure 11-4,
states that the degree of curve is the central angle
formed by two radii that extend from the center of a
circle to the ends of an arc measuring 100 feet long
(or 100 meters long if you are using metric units).
Therefore, if you take a sharp curve, mark off a portion
so that the distance along the arc is exactly 100 feet,
and determine that the central angle is 12°, then you
have a curve for which the degree of curvature is 12°;
it is referred to as a 12° curve.
Figure 11-4.—Degree of curve (arc definition).
11-4