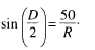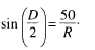By studying figure 11-4, you can see that the ratiodesign speed and allowable superelevation. 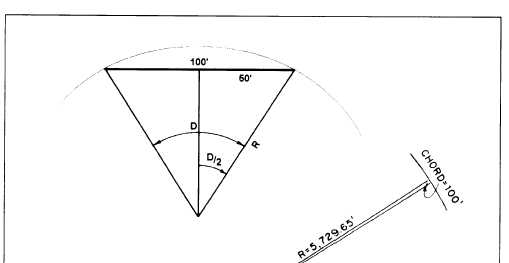Then thebetween the degree of curvature(D) and 360° is theradius is calculated.same as the ratio between 100 feet of arc and thecircumference (C) of a circle having the same radius.That may be expressed as follows:Since the circumference of a circle equalsabove expression can be written as:theSolving this expression for R:and also D:Degree of Curve (Chord Definition)The chord definition (fig. 11-5) is used in railwaypractice and in some highway work. This definitionstates that the degree of curve is the central angleformed by two radii drawn from the center of the circleto the ends of a chord 100 feet (or 100 meters) long.If you take a flat curve, mark a 100-foot chord, anddetermine the central angle to be 0°30’, then you havea 30-minute curve (chord definition).From observation of figure 11-5, you can see thefollowing trigonometric relationship:Then, solving for R:For a 1° curve, D = 1; therefore R = 5,729.58 feet, ormeters, depending upon the system of units you areusing.For a 10 curve (chord definition), D = 1; therefore R =In practice the design engineer usually selects the5,729.65 feet, or meters, depending upon the system ofdegree of curvature on the basis of such factors as theunits you are using.Figure 11-5.—Degree of curve (chord definition).11-5
Integrated Publishing, Inc. - A (SDVOSB) Service Disabled Veteran Owned Small Business
