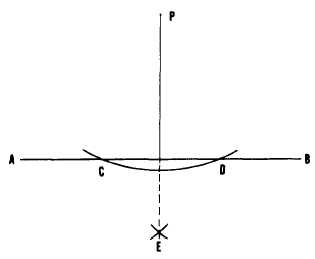
Figure 4-3.-Dropping a perpendicular from a given point
to a line.
Figure 4-3 shows a method of dropping a
perpendicular from a given point to a line, using
a compass. To drop a perpendicular from point
P to AB, set the needlepoint of the compass at
P and strike an arc intersecting AB at C and D.
With C and D as centers and any radius larger
than one-half of CD, strike arcs intersecting at
E. A line from P through E is perpendicular to
AB.
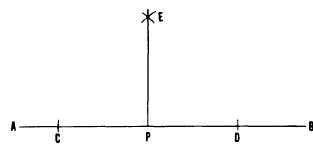
Figure 4-4 shows a method of erecting a
perpendicular from a given point on a line. To
erect a perpendicular from point P on AB, set a
compass to any convenient radius, and, with P
as a center, strike arcs intersecting AB at C and
D. With C and D as centers and any radius larger
than one-half of CD, strike arcs intersecting at
E. A line from P through E is perpendicular to
AB.
BISECTION OF A LINE
A line can be bisected by trial and error with
dividers; that is, by setting the dividers to various
Figure 4-5.-Bisecting a line.
spreads until you find one that correctly measures
one-half the length of the line.
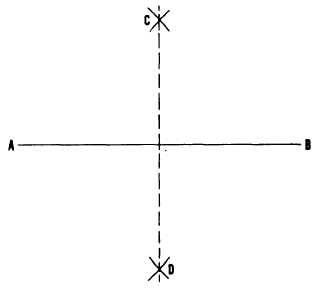
Geometric construction for bisecting a line is
shown in figure 4-5. To bisect the line AB, use
the ends of the line, A and B, as centers; set a
compass to a radius greater than one-half the
length of AB; and strike arcs intersecting at C and
D. A line drawn from C through D bisects AB.
DIVISION INTO ANY NUMBER
OF EQUAL PARTS
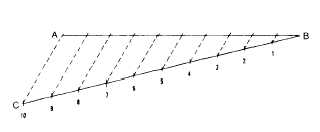
A line may be divided into more than two
equal parts by trial and error with the dividers.
Geometric construction for dividing a line into any
number of equal parts is shown in figure 4-6. To
divide AB into 10 equal parts, draw a ray line CB
from B at a convenient acute angle to AB. Set a
compass to spread less than one-tenth of the
length of CB, and lay off this interval 10 times
from B on CB. Draw a line from the 10th interval
Figure 4-4.-Erecting a perpendicular from a given point on
a line.
Figure 4-6.-Dividing a line into any number of equal parts.
4-2