slightly longer than AB. Use a T square and a 45°
triangle to draw AF and EB at 45° to AB and CD,
Connect AE and FB.
SQUARE IN A GIVEN
CIRCUMSCRIBED CIRCLE
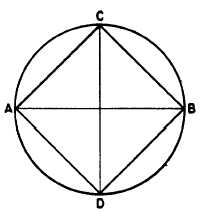
Figure 4-20 shows a method of drawing a
square in a given circumscribed circle. Draw the
diameters AB and CD at right angles to each
other, and connect the points where the diameters
intersect the circumference of the circle.
SQUARE CIRCUMSCRIBED ON A
GIVEN INSCRIBED CIRCLE
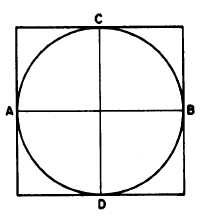
Figure 4-21 shows a method of circumscribing
a square on a given inscribed circle, Draw
diameters AB and CD at right angles to each
other. Then draw each side of the square tangent
to the point where a diameter intersects the
circumference of the circle and perpendicular to
the diameter.
ANY REGULAR POLYGON IN A
GIVEN CIRCUMSCRIBED CIRCLE
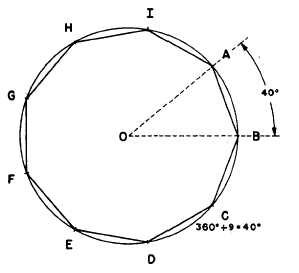
You can construct any regular polygon in a
given circumscribed circle by trial and error with
a drafting compass or dividers as shown in figure
4-22. To draw a nine-sided regular polygon in the
circle shown, divide the circumference by trial and
error with a compass or dividers into nine equal
segments, and connect the points of intersection.
To get a trial spread for a compass or dividers,
divide the central angle subtended by the entire
circle (360) by the number of sides of the polygon,
in this case, by nine. Then, lay off the central
angle quotient from the center of the circle to the
circumference with a protractor.
ANY REGULAR POLYGON ON A
GIVEN INSCRIBED CIRCLE
The same method (dividing the circumference
into equal segments) can be used to construct a
regular polygon on a given inscribed circle. In this
case, however, instead of connecting the points
of intersection on the circumference, you draw
each side tangent to the circumference and
Figure 4-20.-Square in a given circumscribed circle.
Figure 4-21.-Square on a given inscribed circle.
Figure 4-22.-Regular polygon in a given circumscribed
circle.
4-7