corrections should be added as indicated by the
plus signs.
To the right of the “Temp. Corr.” column
is the “Slope Corr.” column. Its entries are to
be subtracted as indicated. Use the following
equation to compute the slope correction.
For the first taped interval, we have an h of 6.0
ft and an s of 100 ft.
Therefore
The slope correction is computed as follows:
Next to the column for slope correction comes the
“Total Corr.” column, containing the algebraic
sum of the three corrections for each taped
interval. Finally, in the “Horiz. Dist.” column,
each value is determined by subtracting the total
correction for each interval from the measured
slope distance for that interval. (This example
used in figure 12-17 happens to be all negative.)
At the bottom of this column, the sum of the
horizontal distances appears. This is the
horizontal distance from station K to station L.
Solving Surveying Problems by Tape
Before the modern instruments used to
measure angles directly in the field were devised,
the tape (or rather, its equivalent, the Gunter’s
chain) was often used. This tape was used not only
for measuring linear distances but also for
measuring angles more accurately than was
possible with a compass.
LAYING OUT A RIGHT ANGLE.— In
laying out a right angle (or erecting a perpendicu-
lar) by tape, you apply the basic trigonometric
theory that a triangle with sides in the ratio of
3:4:5 is always a right triangle.
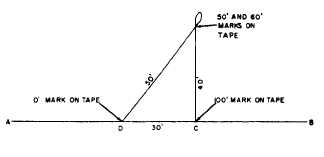
Assume that on the line AB shown in figure
12-18, you want to use a 100-ft tape to run a line
from C perpendicular to AB. If a triangle with
sides in the ratio of 3:4:5 is a right triangle, then
one with sides in the ratio of 30:40:50 is also a
right triangle. From C, measure off DC, 30 ft
Figure 12-18.-Laying out a right angle using a 100-foot
tape.
long. Set the zero-foot end of the tape on D and
the 100-ft end on C. Have a person hold the 50-ft
and 60-ft marks on the tape together and run out
the bight. When the tape becomes taut, the 40-ft
length from C will be perpendicular to AB.
MEASURING AN ANGLE BY TAPE.—
There are two methods commonly used to
determine the size of an angle by tape: the
CHORD method and the TANGENT method.
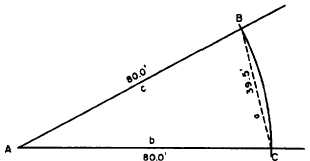
The chord method can be applied, using the
example shown in figure 12-19. Suppose you want
to determine the size of angle A. Measure off
equal distances from A (80.0 ft), and establish
points B and C. Measure BC; assume that it
measures 39.5 ft, as shown. You can now
determine the size of angle A by applying the
following equation:
in which
Figure 12-19.-Determining the size of an angle by the chord
method.
12-21