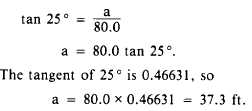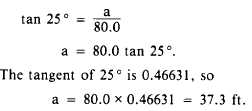First, solving for
we have
Since
Reference to a table of natural functions shows
that the angle with cos equal to 0.87872 measures,
to the nearest 1 min., 28°29´.
The intervals measured off from A were made
equal for mere convenience. The solution will
work just as well for unequal intervals.
In determining the size of an angle by the
tangent method, you simply lay off a right triangle
and solve for angle A by the common tangent
solution.
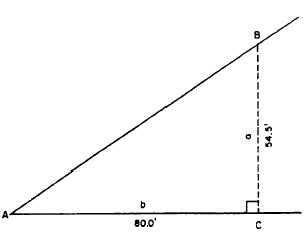
Suppose that in figure 12-20, you want to
determine the size of angle A. Measure off AC
a convenient length (say, 80.0 ft). Lay off CB
perpendicular to AC and measure it; say it
measures 54.5 ft, as shown. The angle is computed
by using the following formula:
The angle with tangent 0.68125 measures 34°18´.
Figure 12-20.-Determining the size of an angle by the
tangent method.
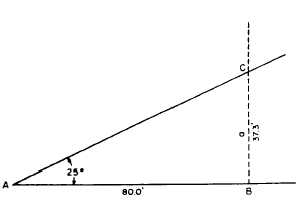
LAYING OFF AN ANGLE OF A GIVEN
SIZE.— An angle of a given size can be laid off
by tape by applying the tangent right triangle
solution. Suppose that in figure 12-21, you want
to lay off a line AC from A, 25° from line AB,
Again measure off a convenient 80.0 ft from
A to establish point B. Erect a perpendicular from
B as shown by the dotted line. You want to
measure off along this perpendicular side a
(opposite side), the distance that, when divided
by the adjacent side, will give the value of the
natural tangent of 25°. Use the following formula:
Measure off 37.3 ft from B to establish point
C. A line from A through C will form an angle
of 25° from AB.
Identifying Chaining Mistakes and Errors
In surveying, distinctions are made between
ERRORS and MISTAKES. Errors are caused by
factors such as the effects of nature, the physical
condition of the personnel performing the survey,
and the condition of your instruments. Mistakes,
however, are simply human blunders. While
errors may be compensated for, mistakes can be
detected, correct, and better yet, prevented only
by the exercise of care.
COMMON MISTAKES.— Mistakes may
result from poor work habits, lack of judgment,
or confusion. They are often costly, time con-
suming, and difficult to detect. The easiest way
to avoid them is to establish a definite procedure
and follow it, being constantly alert during the
Figure 12-21.-Laying off an angle of a given size.
12-22