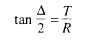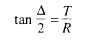Notice that in both the arc definition and the chord
definition, the radius of curvature is inversely
proportional to the degree of curvature. In other
words, the larger the degree of curve, the shorter the
radius; for example, using the arc definition, the radius
of a 1° curve is 5,729.58 units, and the radius of a 5°
curve is 1,145.92 units. Under the chord definition, the
radius of a 1° curve is 5,729.65 units, and the radius
of a 5° curve is 1,146.28 units.
CURVE FORMULAS
The relationship between the elements of a curve
is expressed in a variety of formulas. The formulas for
radius (R) and degree of curve (D), as they apply to
both the arc and chord definitions, were given in the
preceding discussion of the degree of curvature.
Additional formulas you will use in the computations
for a curve are discussed in the following sections.
and solving for T,
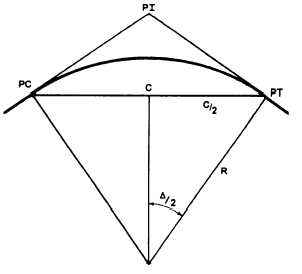
Chord Distance
By observing figure 11-7, you can see that the
solution for the length of a chord, either a full chord
(C) or the long chord (LC), is also a simple
right-triangle solution. As shown in the figure, C/2 is
one side of a right triangle and is opposite angle N2.
The radius (R) is the hypotenuse of the same triangle.
Therefore,
and solving for C:
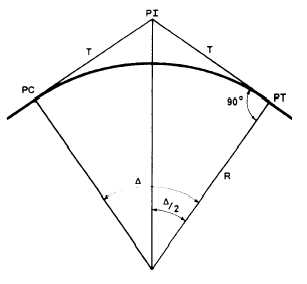
Tangent Distance
Length of Curve
By studying figure 11-6, you can see that the
solution for the tangent distance (T) is a simple
right-triangle solution. In the figure, both T and R are
sides of a right triangle, with T being opposite to angle
N2. Therefore, from your knowledge of trigonometric
functions you know that
In the arc definition of the degree of curvature,
length is measured along the arc, as shown in view A
of figure 11-8, In this figure the relationship between
D, & L, and a 100-foot arc length may be expressed
as follows:
Figure 11-6.—Tangent distance.
Figure 11-7.—Chord distance.
11-6