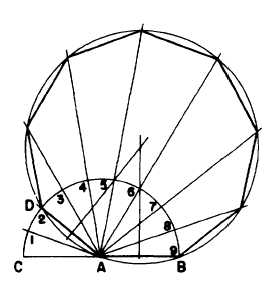
Figure 4-23.-Regular polygon on a given inscribed circle.
perpendicular to the radius at each point of
intersection, as shown in figure 4-23.
ANY REGULAR POLYGON WITH A
GIVEN LENGTH OF SIDE
Figure 4-24 shows a method of drawing any
regular polygon with a given length of side. To
draw a nine-sided regular polygon with length of
side equal to AB, first extend AB to C, making
CA equal to AB. With A as a center and AB (or
Figure 4-24.-Any regular polygon with a given length of
side.
CA) as a radius, draw a semicircle as shown.
Divide the semicircle into nine equal segments
from C to B, and draw radii from A to the points
of intersection. The radius A2 is always the
second side of the polygon.
Draw a circle through points A, B, and D.
To do this, first erect perpendicular bisectors
from DA and AB. The point of intersection of
the bisectors is the center of the circle. The
circle is the circumscribed circle of the polygon.
To draw the remaining sides, extend the radii
from the semicircle as shown, and connect the
points where they intersect the circumscribed
circle.
Besides the methods described for constructing
any regular polygon, there are particular methods
for constructing a regular pentagon, hexagon, or
octagon.
REGULAR PENTAGON IN A
GIVEN CIRCUMSCRIBED CIRCLE
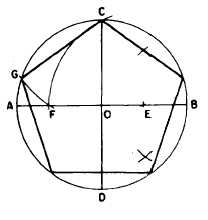
Figure 4-25 shows a method of constructing
a regular pentagon in a given circumscribed
circle. Draw a horizontal diameter AB and a
vertical diameter CD. Locate E, the midpoint of
the radius OB. Set a compass to the spread
between E and C, and, with E as a center, strike
the arc CF. Set a compass to the spread between
C and F, and, with C as a center, strike the arc
GF. A line from G to C forms one side of the
pentagon. Set a compass to GC and lay off this
interval from C around the circle. Connect the
points of intersection.
Figure 4-25.-Regular pentagon in a given circumscribed
circle.
4-8