Figure 7-27.—Second step for tabulated computation of figure 7-24.
Figures 7-26 and 7-27 show the method of
determining the double area from the coordinates. First,
multiply pairs of diagonally opposite X and Y
coordinates, as shown in figure 7-26, and determine the
sum of the products. Then, multiply pairs diagonally in
the opposite direction, as shown in figure 7-27, and
determine the sum of the products. The difference
between the sums (shown in fig. 7-26) is the double area
or 1,044,918.76 – 397,011.37 = 647,907.39 square feet
The symbol shown beside the sum of the coordinate
products is the capital Greek letter (Z) sigma In this
case, it simply means sum.
AREA BY TRAPEZOIDAL FORMULA.— It is
often necessary to compute the area of an irregular
figure, one or more of whose sides do not forma straight
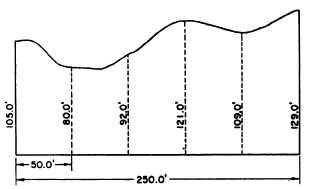
Figure 7-28.—Area of irregular figure by trapezoidal rule.
line. For illustration purpose, let us assume that figure
7-28 is a parcel of land in which the south, east, and west
boundaries are straight lines per pendicular to each other,
but the north boundary is a meandering shoreline.
To determine the area of this figure, first lay off
conveniently equal intervals (in this case, 50.0-foot
intervals) from the west boundary and erect perpen-
diculars as shown. Measure the perpendiculars. Call the
equal interval d and the perpendiculars (beginning with
the west boundary and ending with the east boundary)
hl through k.
Now, you can see that for any segment lying
between two perpendiculars, the approximate area, by
the rule for determining the area of a trapezoid, equals
the product of d times the average between the
perpendiculars. For the most westerly segment, for
example, the area is
The total area equals the sum of the areas of the
segments; therefore, since d is a factor common to each
segment, the formula for the total area may be expressed
as follows:
7-19